Arithmétiques randomisées / améliorées pour la Cryptographie

Recherche des bases d'un système assurant une arithmétique modulaire efficace pour un modulo premier donné

2016-2020 retour haut de page

Dans un travail effectué au sein de l'équipe Algorithmes pour la sécurité des communications du LIP6, nous nous sommes penchés sur la recherche de bases d'un système de représentation qui a fait ses preuves en cryptographie; le système de représentation adapté polynomial, ou Polynomial Modular Number System (PMNS), utilisé pour l’arithmétique modulaire, avec des algorithmes plus efficaces que les méthodes sans division connues telles que Montgomery et Barrett.

En effet, de nombreuses applications en cryptographie sont basées sur de grands corps finis premiers, comme les protocoles Diffie-Hellmann, ElGamal et ECC. Notre but est de proposer de nombreuses bases de ce système en assurant une arithmétique efficace pour un modulo premier donné, chacune avec leurs propres propriétés de calcul. Cette capacité à fournir plusieurs représentations équivalentes est également un point intéressant en termes de performance si l’on veut masquer les calculs pour protéger une implantation contre des observateurs malveillants.

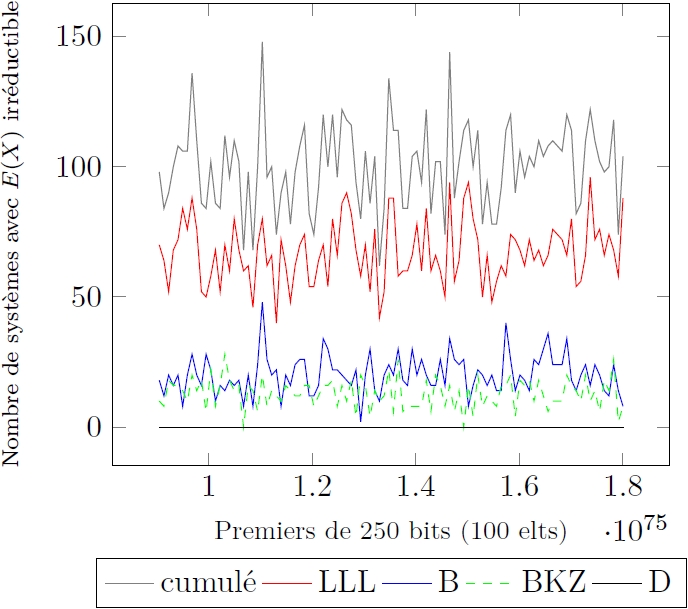
Néanmoins, la construction de ces systèmes est limitée par les paramètres restrictifs du théorème d'existence et la recherche de bases viables n'est pas triviale, conduisant à peu de systèmes en pratique. La construction de tels systèmes est basée sur des polynôme creux, appelés polynômes de réduction, dont les racines sont utilisées comme bases de ce type de représentation positionnelle. L’intérêt de ces polynômes creux réside dans l’efficacité de l’arithmétique modulaire engendrée. Le nombre de systèmes PMNS que nous pouvons générer à partir d’un entier p et d'un polynôme de réduction E(X) est égal au nombre de racines de E(X) dans Z/pZ.

Nous avons apporté des solutions à ces limitations, d'abord via la proposition d'un théorème général d'existence, en garantissant une borne sur les chiffres, qui peut être calculée simplement à partir de la norme 1 du réseau euclidien associé au système. Pour cela, nous proposons trois stratégies pour calculer une base d'un sous-réseau du réseau associé. Ce théorème nous a conduit à considérer les systèmes PMNS définis par un polynôme de réduction irréductible pour lesquels définir une base du réseau associé est aisé.

Puis nous avons présenté des classes de polynômes adaptés pour obtenir des systèmes avec une arithmétique efficace sur les représentations. Enfin pour un premier p, nous avons évalué le nombre de racines de polynômes modulo p afin de décrire le nombre minimum de bases PMNS que nous pouvons atteindre. Ces théorèmes, propositions et corollaires nous ont permis de produire des PMNS avec des polynômes de réduction spécifiques garantissant des réductions efficaces et dont les racines fournissent les bases de ces systèmes.

Nous avons à présent la possibilité d'offrir pour un modulo premier donné une grande variété de PMNS qui peuvent être utilisés efficacement pour différentes applications basées sur de grands corps finis premiers. Nos implémentations permettent la génération et la sélection des systèmes les plus compacts et efficients. À chaque exécution, un système différent peut être choisi.

Valorisations

• 1 revue internationale : Advances in Mathematics of Communications (AIMS), 2022;
• 1 présentation au séminaire du laboratoire IMATH à l'Université de Toulon, 2019.

Randomisation de l'arithmétique modulaire

2018-2020 retour haut de page

Dans un travail en collaboration avec l'équipe d’Informatique et Algèbre Appliquée de l'Institut de Mathématiques de Toulon de l'Université de Toulon, nous avons montré comment utiliser la redondance intrinsèque du système de représentation PMNS pour construire des protections arithmétiques efficaces contre les attaques SCA et les attaques spécifiques de points. En effet, le système PMNS peut devenir très redondant quand la taille des chiffres augmente, laissant suggérer une possible exploitation de cette redondance afin de changer aléatoirement de représentation au cours des calculs, au sein d'une même exécution, pour empêcher tout hypothèse de la part d'un attaquant sur les représentations utilisées.

Nous avons décrit comment randomiser les données en entrée lors de la conversion vers le PMNS via deux algorithmes de type Montgomery et Babaï. Nous avons également introduit deux multiplications modulaires randomisées sur le PMNS. Nous avons démontré la résistance de nos constructions, et avons décrit la génération d’un PMNS en garantissant, pour tous les éléments de Z/pZ, le nombre minimum de représentations distinctes que nous voulons. Nous avons aussi montré comment accéder à toutes ces représentations. À partir d'une fonction générant un polynôme (ou un vecteur) aléatoire, aux coefficients bornés par un entier z, nos algorithmes peuvent génèrer des représentations aléatoires distinctes du même élément modulo un premier p, et suivant une loi uniforme sur l'ensemble fini composé des (2 z + 1)^n représentations obtenues pour chaque sortie possible de la fonction.

Ces méthodes peuvent être utilisées pour appliquer des contre-mesures classiques sur la multiplication scalaire kP} sur les courbes elliptiques. Contrairement à certaines contre-mesures existantes nécessitant une ECSM supplémentaire kR} pour un point aléatoire R}, nous avons montré que la randomisation du processus de conversion suffit à elle seule à protéger les données contre l'attaque de Goubin. Ces résultats constituent une première étape dans l'utilisation de la randomisation des opérations arithmétiques sur le PMNS et ouvrent de nouvelles perspectives dans le domaine des contre-mesures aux attaques SCA.

Valorisations

• 1 conférence internationale : 26ème IEEE International Symposium on Computer Arithmetic, 2019;
• 1 présentation au Workshop on Randomness and Arithmetics for Cryptography on Hardware, 2019.

Introduction d'un système hybride pour améliorer l'arithmétique modulaire pour tout modulo premier

2018-2019 retour haut de page

En collaboration avec deux membres de l'Instituto Superior Tecnico de l'Université de Lisbonne, nous avons proposé un nouveau système hybride pour le calcul modulaire. Le but est d'améliorer l'arithmétique modulaire pour tout modulo premier. L'état de l'art effectué dans ce domaine a mis en évidence que les systèmes proposant une arithmétique efficace sont souvent limités à des premiers spéciaux, avec de fortes contraintes. Bien qu'il soit possible d'implémenter l'addition et la multiplication de façon efficace via le système RNS, ce système se prête moins aux réductions modulaires. L'approche traditionnelle de Montgomery sur ces systèmes exige de revenir dans la représentation classique, une étape impliquant de grandes extensions de bases qui augmentent le coût de la réduction.

Le système hybride Hybrid Position-Residues Number System (HPR), proposé par Bigou et Tisserand, rend les algorithmes de multiplication avec une complexité en temps sous-quadratique viables pour ECC, mais reste limité à des premiers d'une forme spéciale, empêchant d'étendre cette approche aux opérations de groupe sur des courbes elliptiques actuellement standardisées.

Pour répondre à ce besoin d'applicabilité pour les courbes elliptiques, nous avons proposé un nouveau système hybride, nommé HyPoRes, où les nombres sont représentés dans un système PMNS avec les coefficients représentés en RNS. Via un affaiblissement des hypothèses sous-jacentes, ce système atteint une complexité en temps sous-quadratique similaire, et supporte n'importe quelle valeur première, ce qui le rend compatible avec les courbes elliptiques standardisées.

Les résultats expérimentaux montrent que la réduction modulaire de HyPoRes est jusqu’à 1,4 fois plus rapide que les approches basées sur RNS pour les nombres premiers standardisés pour ECC. Ce système rend l’application de petites bases RNS de modules proches d’une puissance de deux, habituellement utilisées en traitement du signal, viable pour les applications cryptographiques. De plus, puisque ce système réduit la complexité des extensions de base par rapport à une approche purement RNS, il se prête mieux au parallélisme à une plus petite échelle. La possibilité de généraliser le polynôme de réduction permet également d'introduire des représentations redondantes, obtenues par des changements de systèmes, procurant une protection contre les attaques SCA.

Valorisations

• 1 conférence internationale : 26ème IEEE International Symposium on Computer Arithmetic, 2019;

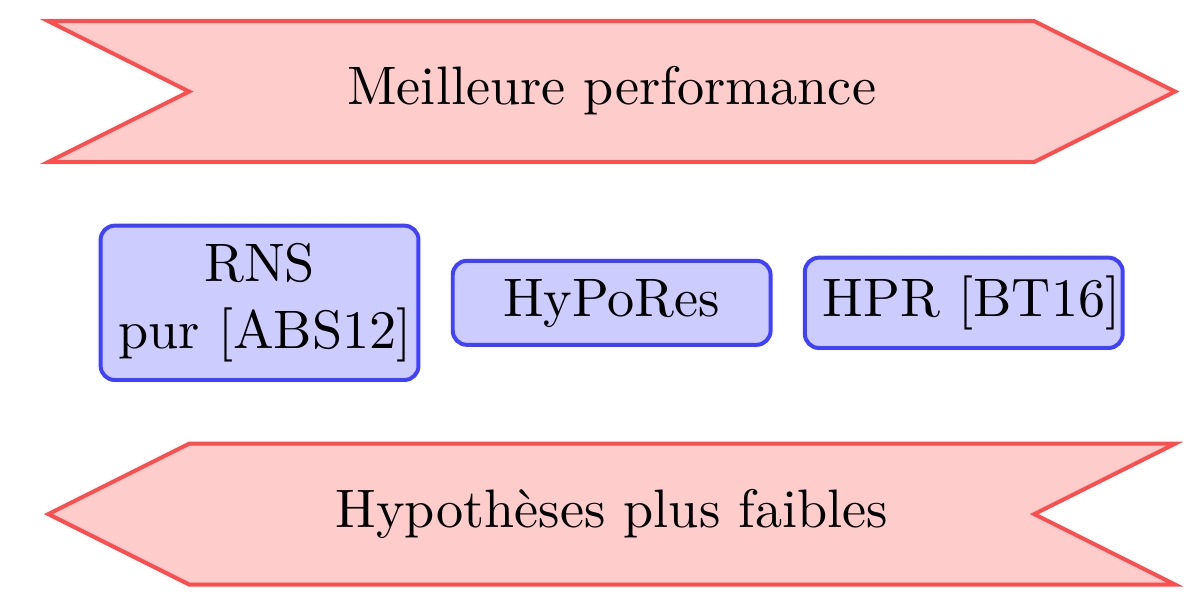FIGURE 3 - Comparaison qualitative du système HyPoRes avec l'art associé.